Explanation of New Roto Standings

Introduced in Season 9 (2016)

The new roto standings estimate a team's odds of winning a particular category against a random opponent. The mean and standard deviation of teams' weekly totals are used to estimate a probability distribution for each team. These distributions are compared to calculate the probability that a randomly selected point from one distribution is greater than a random point from another.

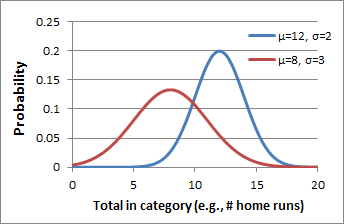
To illustrate, the following graph displays probability curves for two fictional teams. The blue team has a mean of 12 and standard deviation of 2, while the red team has a mean of 8 and standard deviation of 3. To compute the blue team's roto score, we calculate the probability that a random point taken from the blue curve is greater than a random point from the red curve.

Scores are calculated using the formula derived below:

Say we have two teams, (a) and (b), with corresponding probability distributions in a given category.

We are interested in P(x_a>x_b) = P(x_a-x_b>0), where x is a point selected randomly from the indicated distribution.

Assume both distributions are normal and independent. The difference between a random point from the first and a random point from the second, x_D=x_a-x_b , will also be normally distributed, with the following properties:

The mean is the difference between the two teams' means: μ_D=μ_a-μ_b
The variance is pooled: σ_D²=σ_a²+σ_b² , and therefore the standard deviation σ_D=√(σ_a²+σ_b²)

Define the z-score for a given value of x as the number of standard deviations from the mean: z_D=(x_D-μ_D)/σ_D

When x_a-x_b=0, x_D=0 and z_D = (0-μ_D)/σ_D = -(μ_a-μ_b)/√(σ_a²+σ_b²)

Then P(x_a-x_b>0) = Φ(z_D) = Φ((μ_b-μ_a)/√(σ_a²+σ_b²)), where Φ is the integral of the standard normal distribution from z to ∞.

Calculate P against all opposing teams and average the resulting probabilities to estimate the odds of winning the category against a random opponent. This is the roto score for team (a).

Note: When a category is inversely scored (e.g., a lower ERA is better), the roto score is 1-P.

The final equation is: P(x_own > x_opponent) = Avg_i{ Φ((μ_i - μ_own) / √(σ_i² + σ_own²)) } where i is an index of the set of all opposing teams, and Avg is an operator meaning "average of the following set."